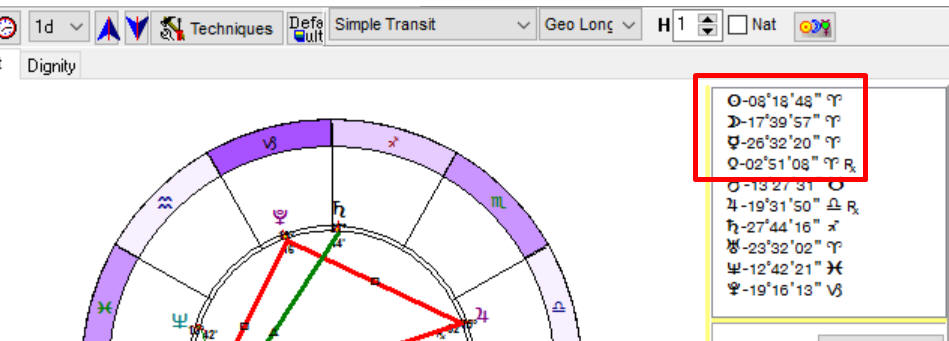
Averaged Longitude

How to calculate the averaged longitude of several planets?

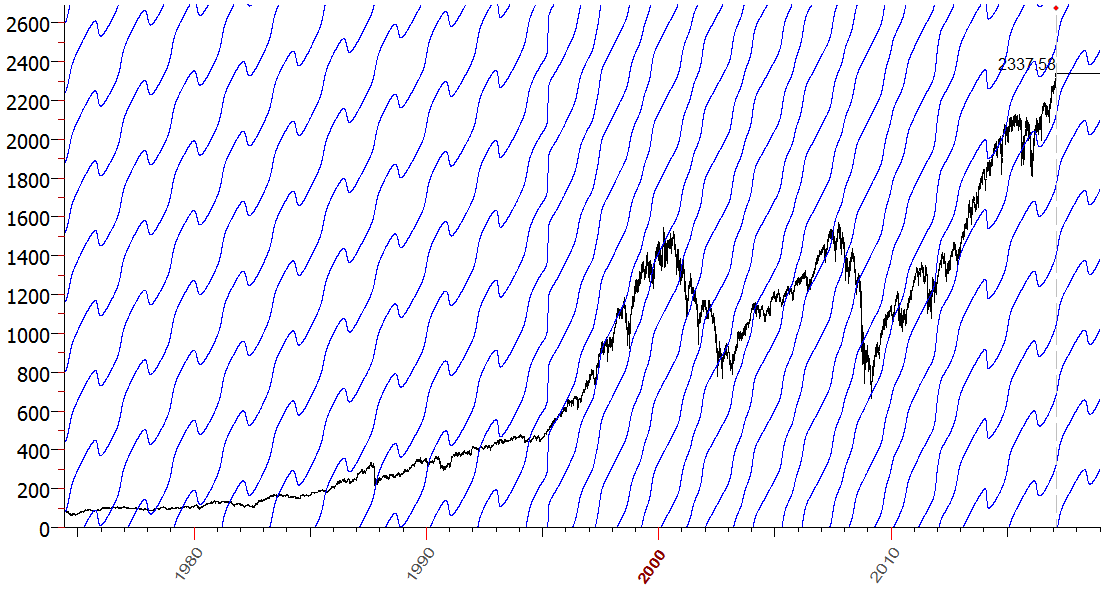
Suppose we want to calculate the averaged longitude of the Sun, Mercury and Venus for this chart: 

There are two ways to make these calculations:

1) Simple calculation algorithm:

We calculate the mean of planetary longitudes. In this particular case this formula looks this way:

(Sun+Mercury+Venus)/3=(8.32+26.53+2.85)/3=12.58=12deg34min of Aries

Here we use 0..360 scale, i.e. 2 deg. of Scorpio=242 degrees.   

Everything is simple here, but there is one side effect in these calculations.  Let's create (Sun+Mercury+Venus)/3 with Timing Solution.  Run extended version and in Options->Customize Object create this object in "Planetary Picture" tab:

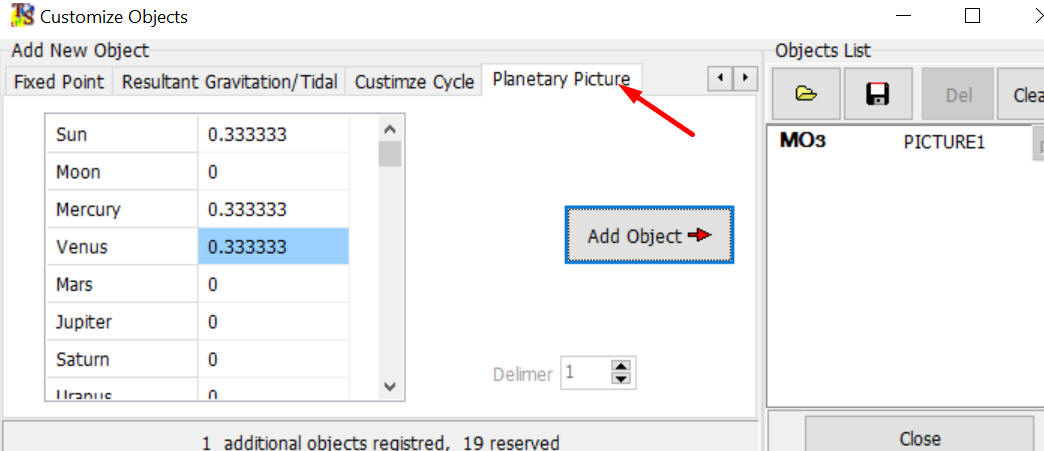
This is planetary picture 0.33333*Sun+0.33333*Mercury+0.33333*Venus

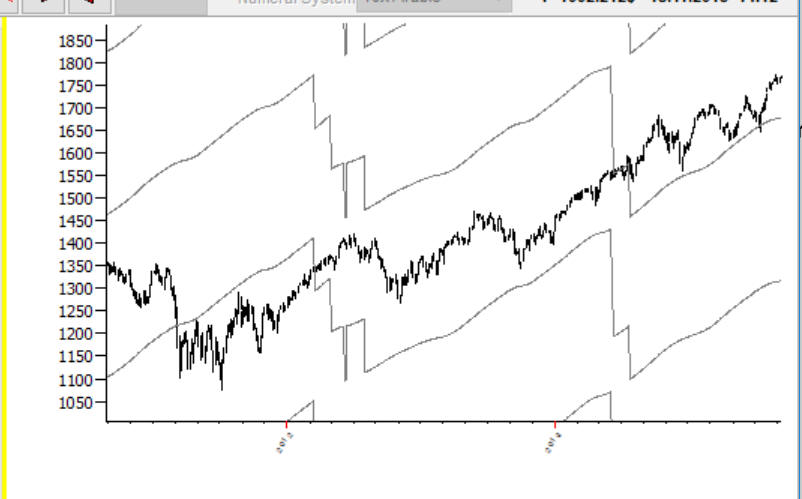
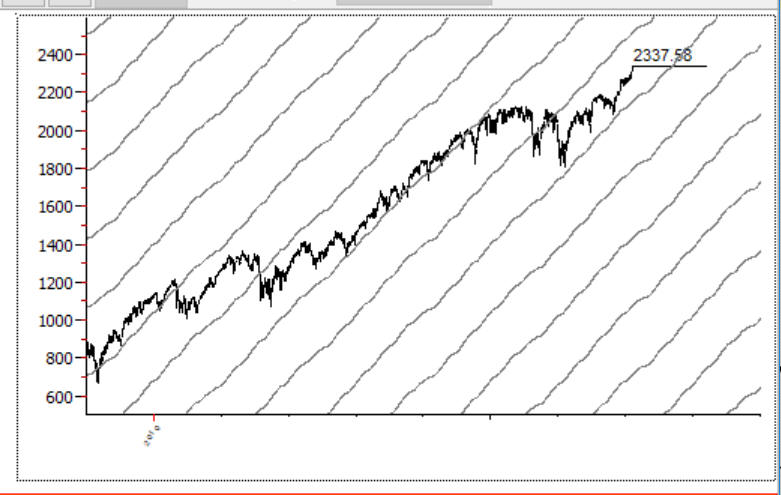
But the planetary picture calculated this way has side-effect: jumps in longitude. For this planetary picture we have 120 degrees jump. These are planetary lines for this planetary picture:

2) Vector arithmetic algorithm

There is another algorithm that is based on vector algebra. We build three vectors for Sun OA, for Mercury OB and for Venus OC:

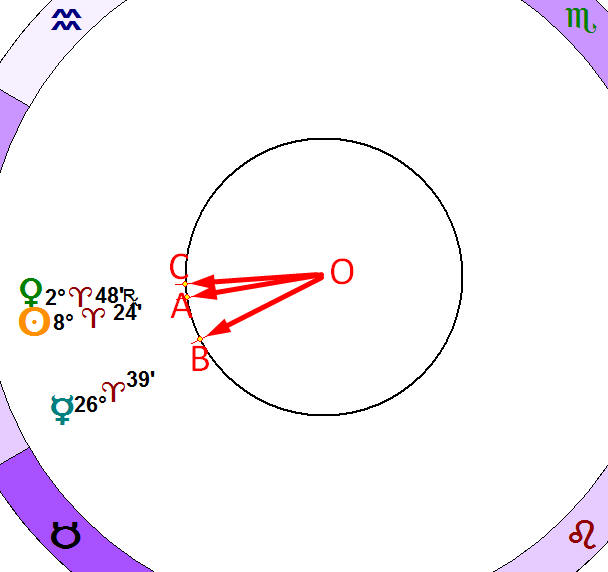
and using rules of vector algebra calculate superposition of these three vectors. I will show how you can do these calculations geometrically.

Firstly calculate superposition of Sun and Mercury vectors (this vector corresponds to the midpoint between these planets):

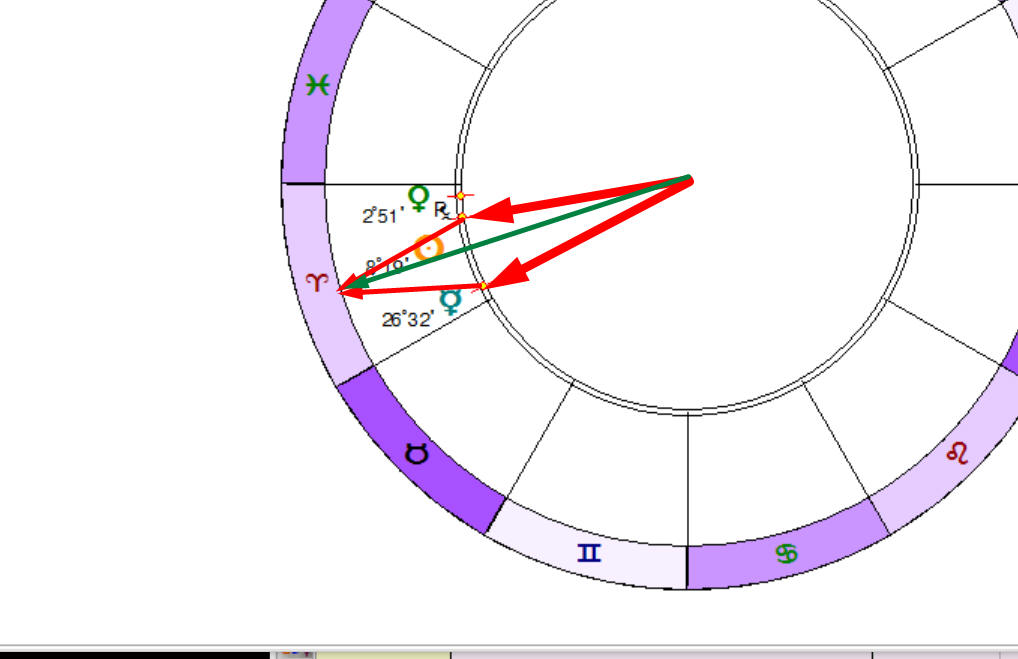
and after that calculate the superposition of this midpoint vector with Venus vector:

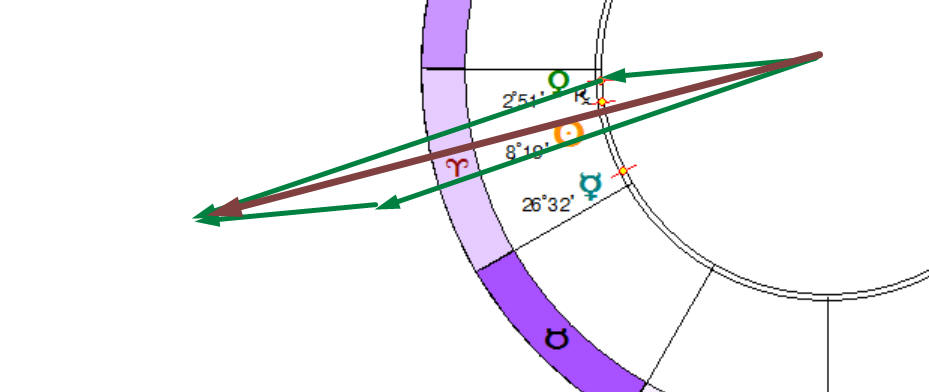
In Timing Solution we call a vector calculated this way - information vector. The longitude for the information vector looks much more logical, the jumps in the longitude happen very seldom.

Here they are, planetary lines for longitude (Sun,Mercury,Venus) information vector:

In Timing Solution you can build information vector through Customized object feature. In "Resultant Gravitation/Tidal" tab, highlight "Information vector" item, choose the planets that form this vector and add this object to "Objects List":

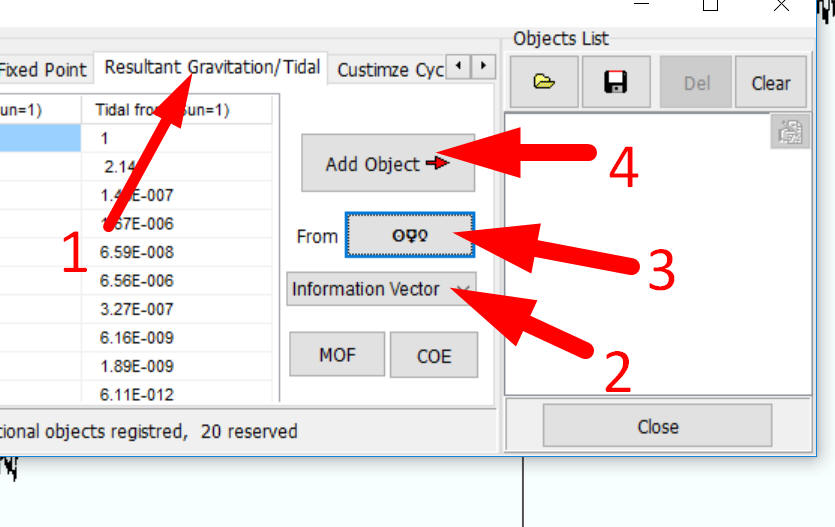
Information vector calculates similar way as resultant gravitation or tidal force. You can take information vector as kind of gravitation force but it is the same for all planets and does not depend on distances.

As an example, I have calculated planetary lines for mean (Sun,Mars,Jupiter) longitude:

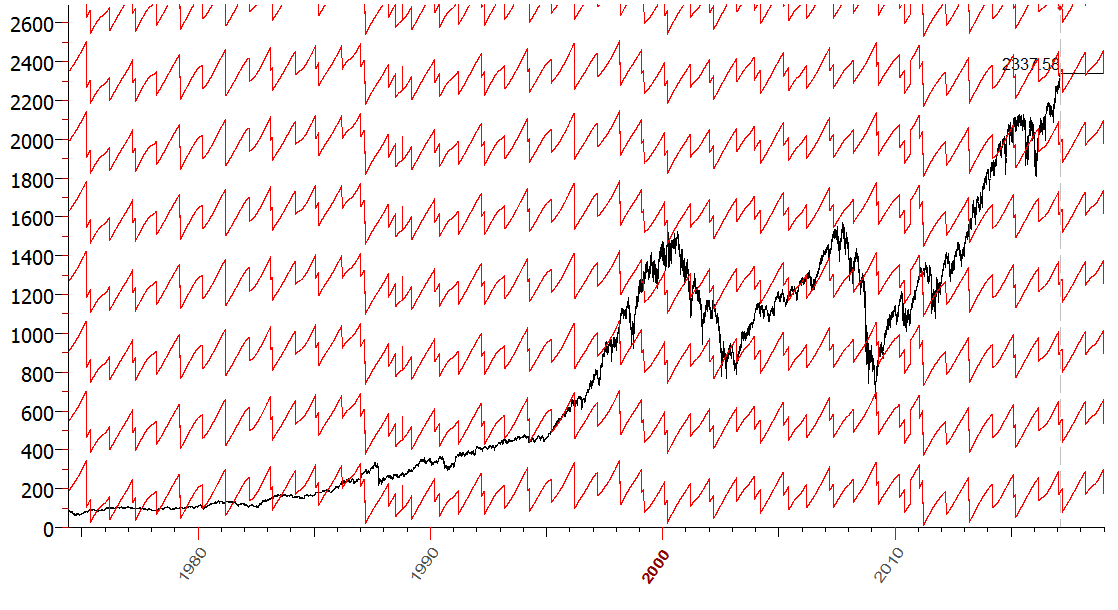
You see, there are lots of jumps here. You can improve these planetary lines applying for them 3H harmonic:

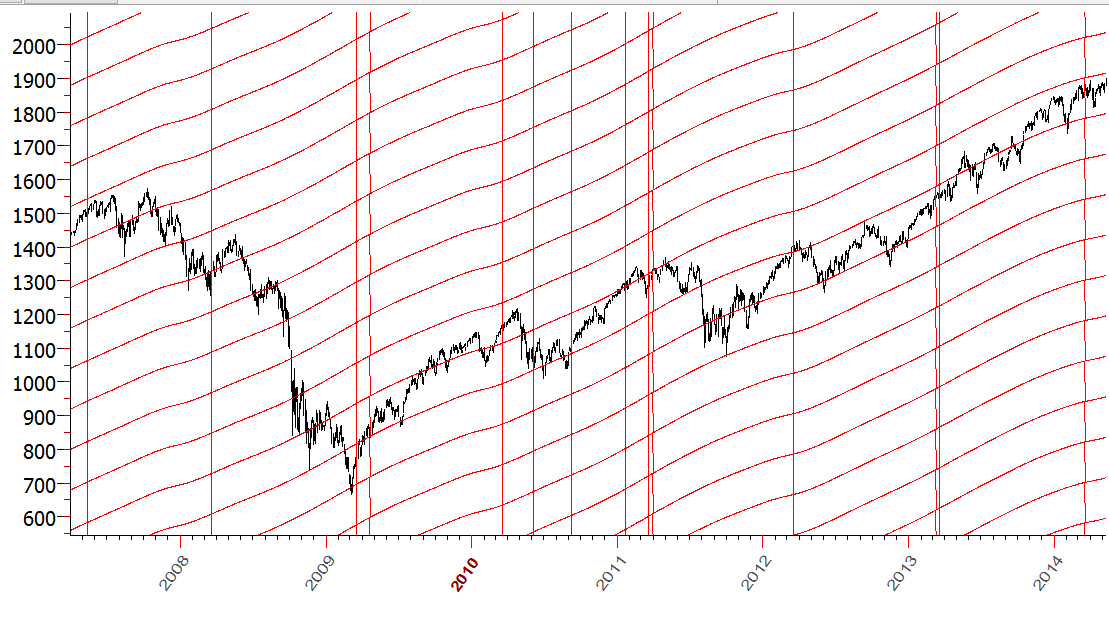
Vertical lines here show jumping dates.

And (Sun,Mars,Jupiter) information vector: