Astronomical scales as a key to understanding the price chart
What this article is about
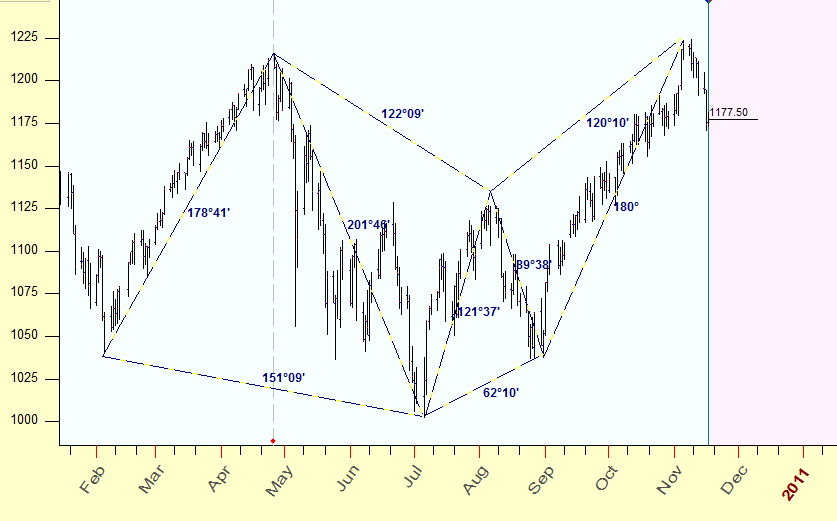
In this article you will find the technology of revealing geometric patterns like the one shown below. Pay attention to the fact that the length of all lines is measured in degrees as these lines are based on planetary positions. Moreover the majority of the lines that serve as the sides of this figure have lengths that correspond to classical astrological aspects of 60, 90, 120, 150 and 180 degrees:.

Therefore the pattern you see here is not just some geometric figure, the sides of this figure are formed by harmonic angles, i.e. astrological aspects. And this is very important; it means that we can work with charting tools that have scales based on some natural measures (I would say - organic charting tools). It is important because it gives us a way to avoid problems related to using the same sheets of paper to scale the price chart as W. D. Gann used to have when drawing his charts. I have nothing against W. D. Gann or the paper he used. The only thing is that the fractal analysis of Dow Jones Industrial Index definitely shows that the fractal nature of DJI in 1900-1950 is totally different from what we have nowadays. (I refer here to R/S analysis that is used to calculate the period of the stochastic cycle; within this period the stock market totally changes its structure). W. D. Gann did a revolutionary step at his time, he made a clear connection between the market moves and moves of the celestial bodies. And he did that at the time when practically a pen and a paper were the only tools for a trader. Nowadays, it is a different story. Electronic trading systems, trading robots, new financial instruments totally have changed the landscape of the time-price Universe. It means that, with all due respect to past achievements, we have to go further, we have to study, and we have to research.
One more important thing is that this approach allows to calculate easily support/resistance cycles, like these ones:
These cycles correspond to the most harmonic places on the price chart, i.e. to the most probable places where the trend can be changed. It is quite possible that the application of astrological approach to Technical Analysis brings some order to the ocean of different charting tools and indicators.
So, this article is about charting tools with the astrological twist. Such tools are presented in Timing Solution software, so all examples and explanation will be done with this software. I hope it will be useful for all of you, users and not-yet users of TS. For TS (Timing Solution) users, this article is an additional explanation of the things that they already know. You will find here some technical notes on how to create these charting tools I use the italic font for them. These notes are for TS users, so you may skip them.
Basic idea
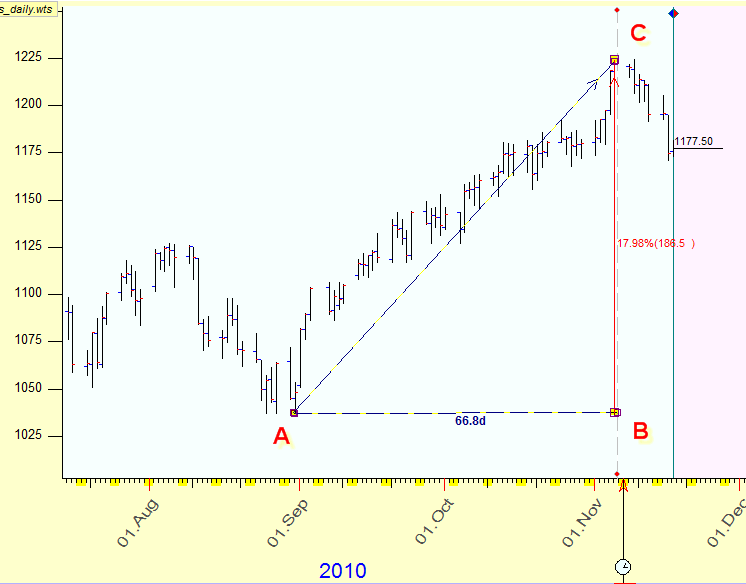
Ask yourself a simple question: How to calculate the time-price distance between two turning points on the price chart? For example, you would like to find the distance between two turning points - A: August 30, 2010 and C: November 5, 2010. Let's do it for S&P500 futures daily data.
If we would do it a hundred years ago (even 50 years ago), we would be fine with the scaled paper. We would put there on the horizontal axis the time scale (calendar or trading days) and some price scale on the vertical axis. And the actual length of a segment used for scaling would be extremely important. It should be adjusted to the analyzed financial instrument - this is the core of scaling and the core of using many Technical Analysis charting techniques. Because many charting techniques actually look for geometrical relations between chart's elements, it is important not only to mark 1 segment of the vertical axis as = $1 and 1 segment of the same (or another) length of the horizontal axis as =1 day; it is also important that everybody uses the same length for these segments (like 1cm = $1 and 1 day). (This is the reason why some teachers of the past century have provided their books or courses with empty paper sheets graded accordingly to the teachings: if you would scale your axis using the segment just 1-2 mm longer than I or assign some other value to a segment, - your results could be dramatically different. from mine.)
Let say that we all would use the same scaled paper. Our turning points are separated by 67 days distance in time and 186.5 points of price change. In other words, the distance between these two turning points is 67 horizontal scale units and 186.5 vertical units. (If somebody uses some different scale, the look of his chart would be different, while the math is still the same.) Now we can apply Pythagorean theorem to calculate AC distance:
This distance is 198.23563 units. Can we use this information somehow to forecast the price?
Before answering this question, let's look at some variations of applying time-price distances to trading.
How to do it with Timing Solution
We recommend "2D Day-Price distance" charting tool to calculate the distance between two turning points, it is here:
Dragging the mouse cursor from one turning point to another, you will see the distance between these points:
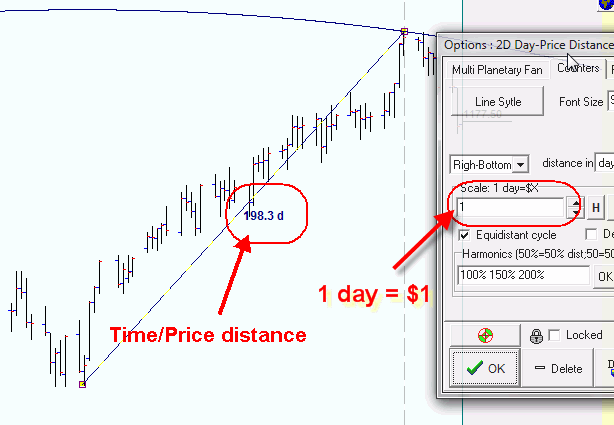
Remember that this is not a separation in time only. This distance incorporates the price as well. The most important parameter here is the price scale, the size of the vertical scale's segment and its relation to a horizontal segment (which is time). So far we set it to 1.0.
Why do we need equidistant cycles?
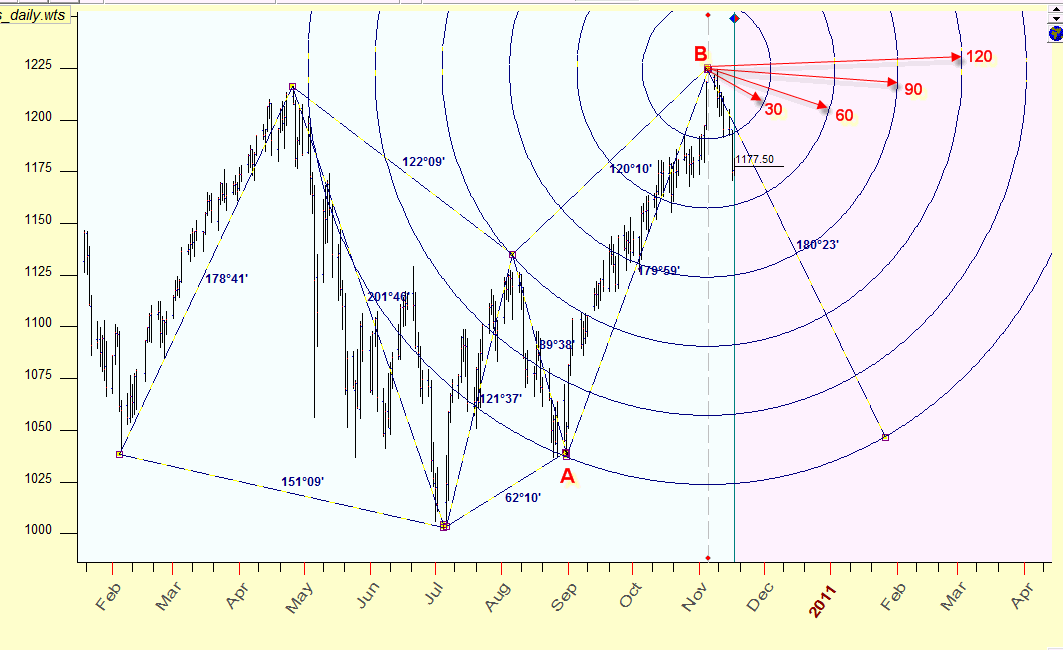
Equidistant cycles are the most obvious application of the time/price idea. Here you can see the equidistant cycle with radius 198.3 days, the center of this cycle is the turning point A (August 30, 2010):
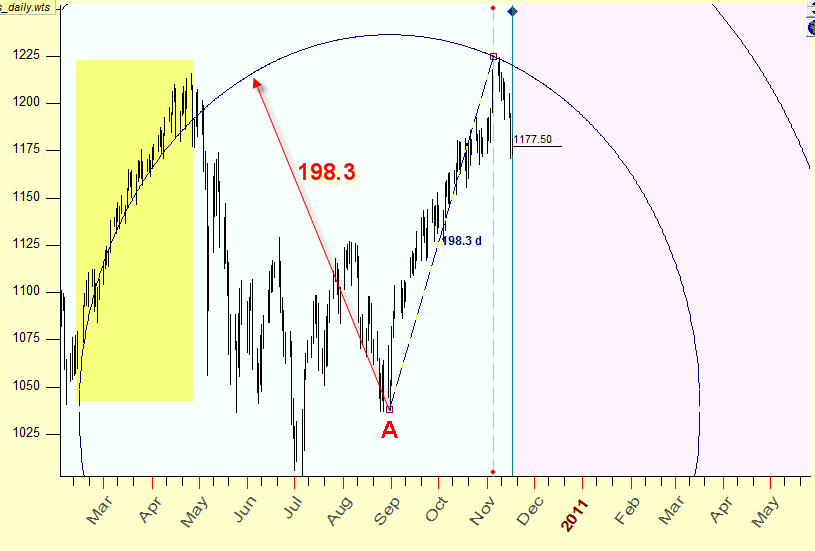
As you see this cycle is tied with the up tend movement in February-April 2010; it is possible that these events are connected somehow.
To illustrate how the equidistant cycles can work in trading, I have created two additional cycles with the center in the turning point A, with a half and one third of AC radius; here they are:
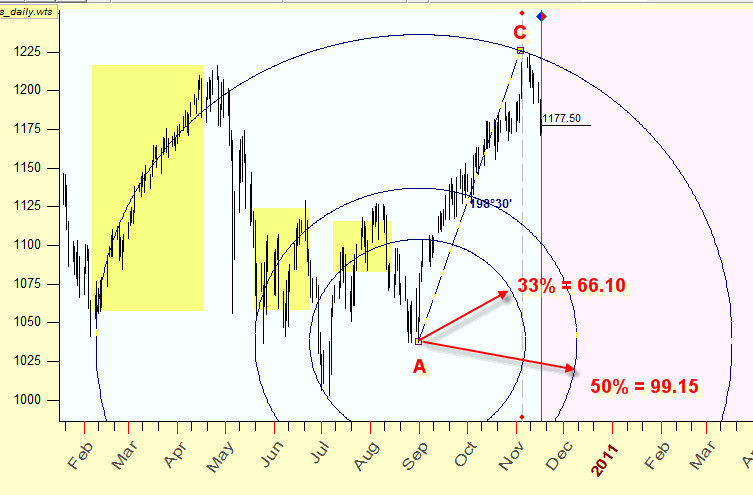
Some people assume that the fractions of the trend's cycle may indicate other periods of similar trend.
I do not think that these cycles can be used by themselves for the forecast, my only purpose is to illustrate that some regular patterns exist in time-price Universe.
How to do it with Timing Solution
It is very easy to draw additional cycles (we call them harmonics), simply type in the charting tools options what harmonics of the radius you want to display:
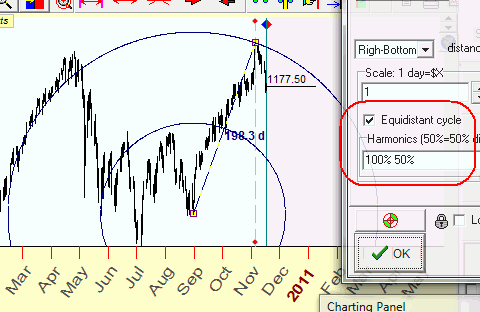
If you do not need to display equidistant cycles, simply uncheck this
option: ![]()
Why do we need scaling?
The previous example was done for S&P 500 futures. Let us do the same for Dow Jones Industrial index. Within these same 67 days, DJI has gained $1500. If we use the same vertical grid scaled for $1, our paper becomes very inconvenient for charting. Mathematically if we apply the Pythagorean theorem to a right triangle with sizes 67 and 1500, we would get the distance between these turning points equal to 1501.5 units, i.e. practically equal to the price change. The price dominates here.
To handle this situation, we have to use a special scale for the price, i.e. to adjust the size of a vertical grid segment to make this chart readable. For example if we assume that 1 segment of the vertical axis corresponds to $10 of the price change - we get the length of the hypotenuse equal to 164.3 grid units:
You can set the scale value in the charting tools options (this is the size of the vertical grid):
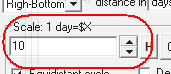
See how the equidistant cycle with the scaled price (Scale=10) looks:
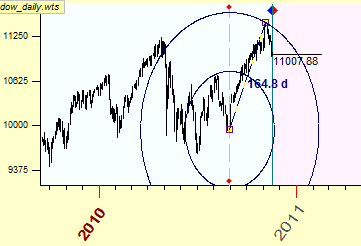
If we apply the scale1 unit=$1, we get these equidistant cycles:
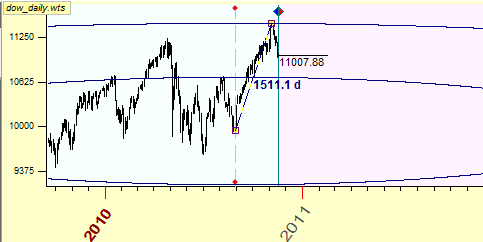
This very long ellipse indicates that the scale for the price is not set properly, i.e. the traditional grid that is used for our paper is not convenient. The time factor is underestimated here, equidistant cycles look like parallel lines. Meanwhile our goal here is to perform timing and pricing together, to make time-price Universe alive. With old-time scaled paper, we cannot do it for modern stock market. We have to do adjustments (scaling), and it is quite probable that the scaling is needed not only for each financial instrument individually but for the different time periods for the same financial instrument as well.
Planetary metrics: a natural measure
Now we have to make a very important move - including astronomical factors in our time-price Universe. This approach opens us the doors to Classical astrological techniques and brings a new vision of abstract mathematical figures.
(If you have noticed, in the very beginning of this article I have promised you the charting tools with astrological twist, and here I speak about astronomical factors. It is not a mistake. Astronomical factors are a standing base for astrological speculations. However, it is astrology that historically happened to be more concentrated on looking for connections between moving physical objects in the space and our ordinary human activities.)
The first step in this direction is to introduce a special time measure. In our conventional life we used to deal with the time measured in years-days-hours-minutes-seconds. However, we can use instead the time based on a planetary movement. It is the same time, only we measure it in degrees of planetary travels. There will be no years-days-hours, though there will be minutes and seconds and degrees as well; these will be minutes and seconds of the arc. It is the same thing as using either kilometers or miles to measure the distance between Toronto and New York City; the distance is the same.
The good part is that we can use angles as a measure, and these could be any angles. As an example, I will use the same two turning points as above. And I look at the Sun, It has traveled from August 30, 2010 (our turning point A) to November 5, 2010 (the point B), and it has passed 65.degrees and 31minutes of its arc. So, instead of days and hours, we can use this angle as a measure of time. Because it is the Sun's path, let call this the Sun time. We can calculate the Moon, Mercury, Venus etc. times in the same manner. As the mathematicians would say, we use here a special metric for our Universe. We use it as an alternative to the Newtonian space-time Universe though we look at the same events. We use it in hope to find some Order in the stock market's Chaos.
So, if we still would be in no-computer era, we could use the paper with the grid. But - we would use a special horizontal grid there: speaking of the Sun time, we would mark there the moments when the Sun ingresses each and every Zodiac sign. Something like this:
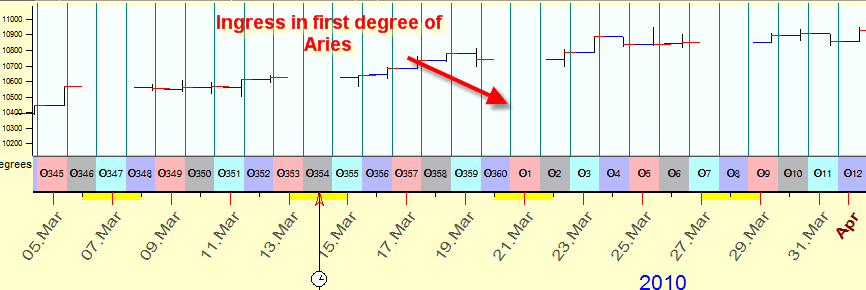
Such kind of a paper is very convenient for astrologers, they can easily see the moments when the Sun ingresses any place of Zodiac.
The main difference with the conventional time is that our astronomical time is irregular. See how the grid based on Mercury's traveling path looks:
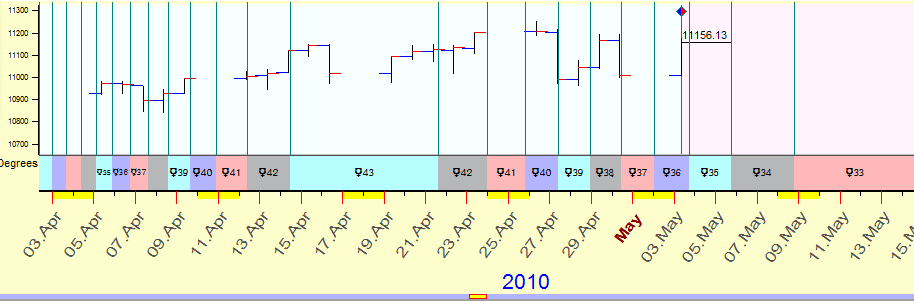
Now, we can add the vertical dimension to the grid.
And here the question arises: what scale should we use for the price? And the answer comes from W. D, Gann: assume that the correspondence exists between the price change and some planetary movement and use this correspondence. For example, we may assume that for the financial instrument in question $1 corresponds to 1 degree of the Sun movement. And we will use the scale based on this assumption. The classical technique that is used the price scaled in accordance to the planetary positions is planetary lines technique. It is used to reveal support/resistance levels. Here is an example of Mercury planetary lines:
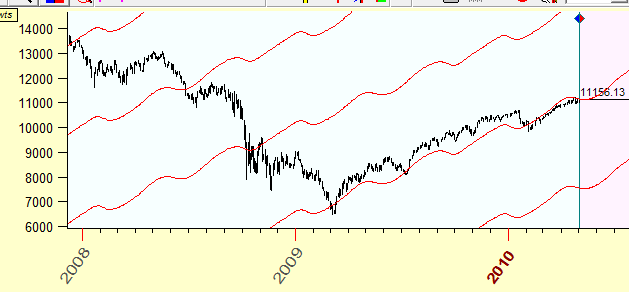
You see here that up trend market moves coincide with these Mercury lines. (Do not use this as a trading hint; please read the article to the end first! There are some tricks that you should know about.)
It means that this technique allows to resolve time/price Universe in other way.
Let's go back to our example. Now we calculate the distance between those two turning points using the Sun time. The Sun has moved within this period for 65deg 31min of the Sun arc. The price change is $185.5. So, if we assume that $1 corresponds to 1 degree of the Sun movement, we have this picture:

And we can calculate the time-price distance between turning points applying Pythagorean theorem:
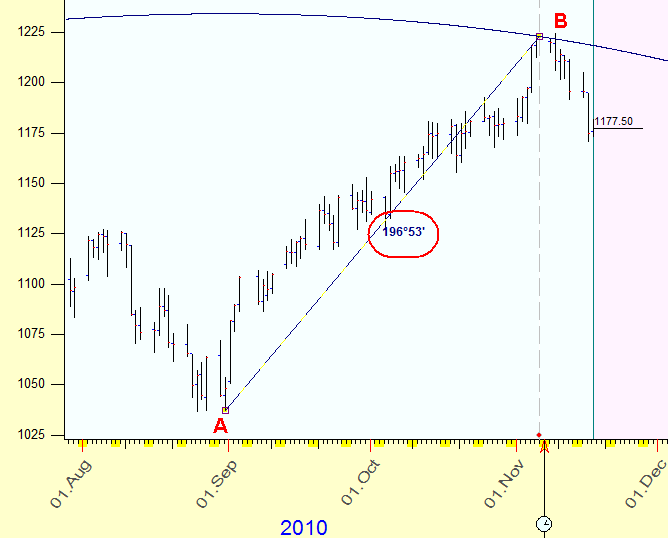
Remember that we measure this distance in degrees of the Sun movement; this brings a new sense to the abstract mathematical digits. Now the fractions and multiplications of the cycle have a precise astrological meaning: 360 degrees is a full cycle, 180 degrees is the aspect of opposition, 120 degrees is a trine etc. We will use this fact a lot, we need it to create models to forecast the market behavior.
Key scale: the door from pure math to astrology
Now we came to another very important moment; it is the core idea of this technique. As you see, in our example the time-price distance between these two turning points is 196 degrees of the Sun's arc. This angle has no meaning from the astrological point of view: the closest significant angle (aspect) is 180 degrees. Astrologers would expect that the distance between two turning points should be some harmonic angle - like 360, 180, 120 .. degrees. If we would have something close to these figures, we can apply the astrological knowledge.
However, this is not the end. There is something we could do. The first thing that comes to mind is to play with the scale. Do you still remember that we have chosen the correspondence between the price and the time assuming that $1 = 1 degree of the Sun movement? What if we make some other assumption? We can take the whole time-price distance between these two turning points exactly as 180 degrees, i.e. the opposition aspect. It means that we have to set the scale for the price equal to 1.114015169, i.e. 1 degree of the Sun movement corresponds to $1.114015169 price change. And we get the exact opposition:
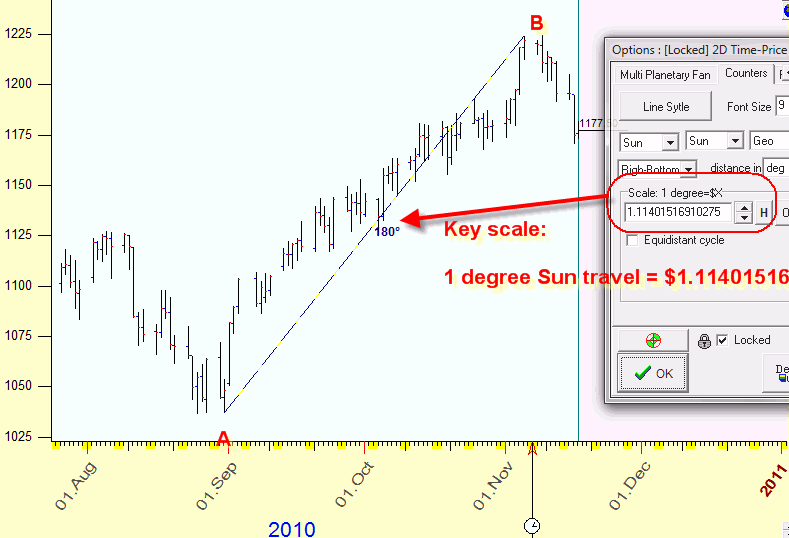
Let's name this new scale as key scale. The key scale can be any number, not the whole digit only.
Another possibility is to play with planets and their combination: instead of the Sun movements, consider movements of the Moon (the Moon time), Mercury (Mercury time) etc. or try to apply heliocentric system.
Key scale verification
So far everything looks as some mathematical exercise. It is time to demonstrate how it works in practice.
Look at the picture below. Here I have calculated the time-price distance between major turning point of the year 2010 using the Sun metric and the price scale of 1.114015169.
You see here that all these distances - except one only (201 degrees) - correspond to classical astrological aspects: opposition (180), trine (120), square (90), sextile (60) and one quincunx (150):

In other words, 6 major turning points of the year 2010 form harmonic distances between each other related to classical astrological aspects. But - and this is really important - these aspects exist in time-price Universe. Here we consider time and price as one universal entity. The astrology gives us a key for a synthesis of the time and the price.
This is very important thing as this key scale provides harmonic patterns for the last 6 turning points. It means that this scale is appropriate to use (for this financial instrument)..You should always check your key scale and the planetary combination using several turning points, the more the better. This is a kind of preliminary back testing of your models.
How to use this technique
The fact that turning points tend to form harmonic distances in time-price Universe allows us to construct prediction tools. The idea is very simple: draw equidistant cycles (using the Sun as a time measure and scale for price 1.114. - if we apple the Sun time). Then use harmonic radii that correspond to classical astrological aspects, i.e. 30, 60, 90, 120, 150, 180 degrees. they will show areas of possible turning points. Here they are:

These cycles show us potential turning points in time and price.
How to do it with Timing Solution
To draw equidistant cycles and calculate the distance using planetary metrics, I recommend to use "2D Time-Price planetary distance" charting tool. It is here:
Dragging the mouse cursor you calculate the distance between two anchor points on the price chart. In charting tools options, define a planetary combination to calculate the distance, the price scale and radii for the equidistant cycles:
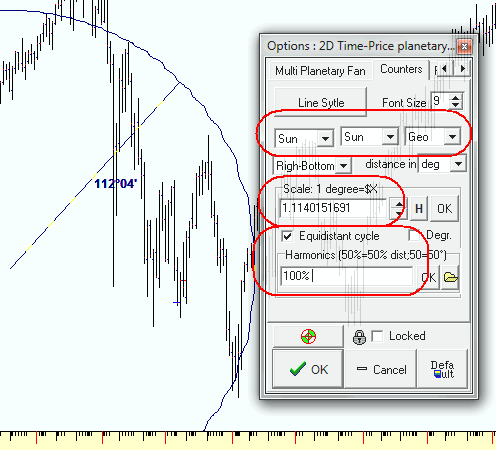
Note: if you type the values for radii 30 60 90, the program will draw equidistance cycles with radii 30 degrees, 60 degrees and 90 degrees. If you type there 50% 100% the program will draw full cycle (100%) with a radius defined by two anchors and half of this radius.
You can use mixed values of % and degrees together:

Using "H" button in charting tools options you can find the price scales that correspond to harmonic angles:
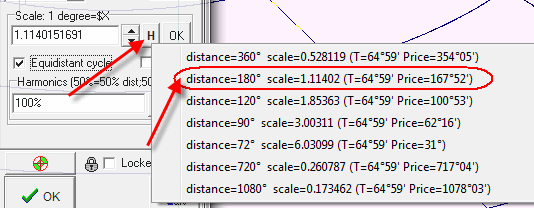
In this example the program indicates that by setting a scale for the price as 1deg=$1.1142 you will get the distance between the anchors equal to 180 degrees. If you set the scale 1deg=$0.528 you will get the distance of 360 degrees.
Take these values as candidates to the role of a key scale. And remember: you have to check your key scales on several turning points.
If you like your settings, click "Default" button to use these parameters "by default":
Next time when you run this charting tool these options will be set "by default". This is convenient when you draw many "2D price-time ..." lines with the same scale, as in our example (I used through the article the Sun lines with the price scale of 1.1142).
There is another way to find a key scale: use multi selection option. In order to do that, follow these steps:
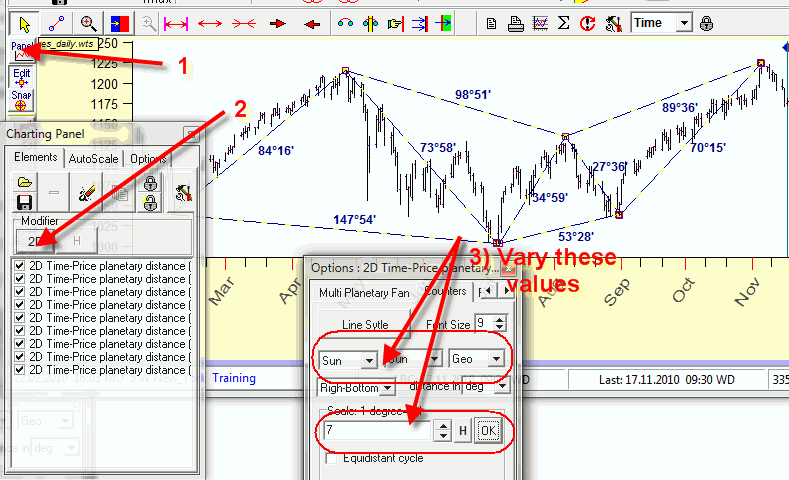
1) open "Charting panel" window;
2) click there "2D" button;
3) vary the scale and try different planetary combinations/Zodiacs. While you vary these parameters, the program automatically recreates the chartings tool, and you are able to see the distances there.
BTW using different planetary combinations you can get very interesting equidistant cycles. As an example, look at these Mars equidistant cycles:
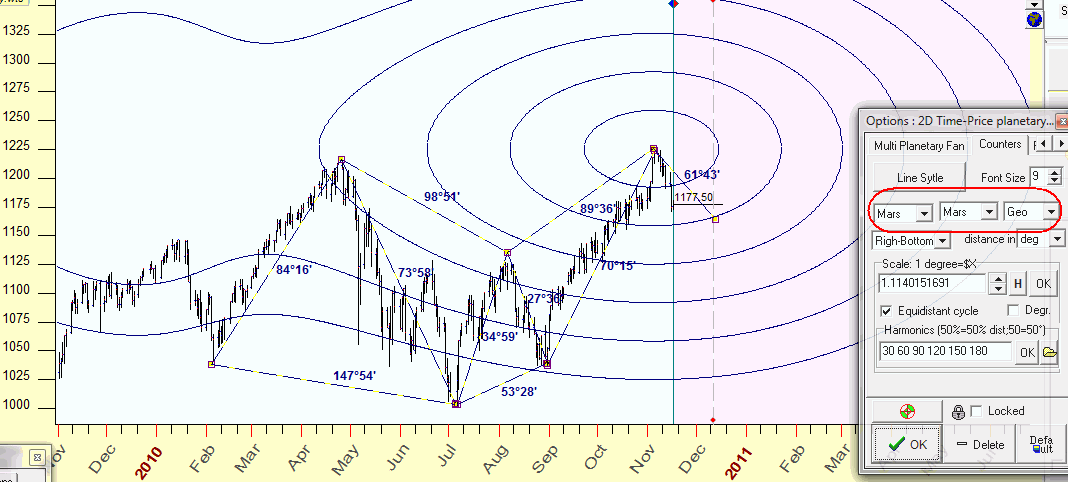
To create this figure, I clicked "2D" button and changed the planetary combination, and now we can see the angles that are formed by this figure and the important points that these equidistant cycles hit (this is just an example):
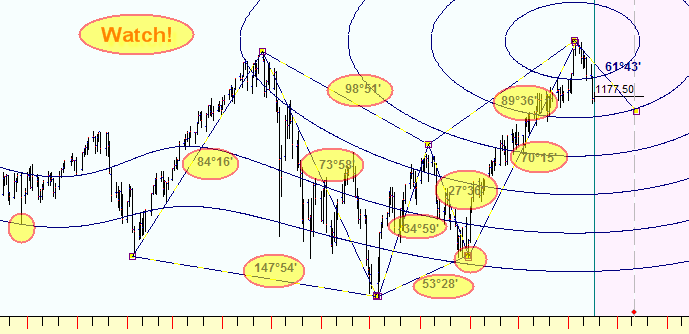
This is an example of Mercury-Mars equidistant cycles:
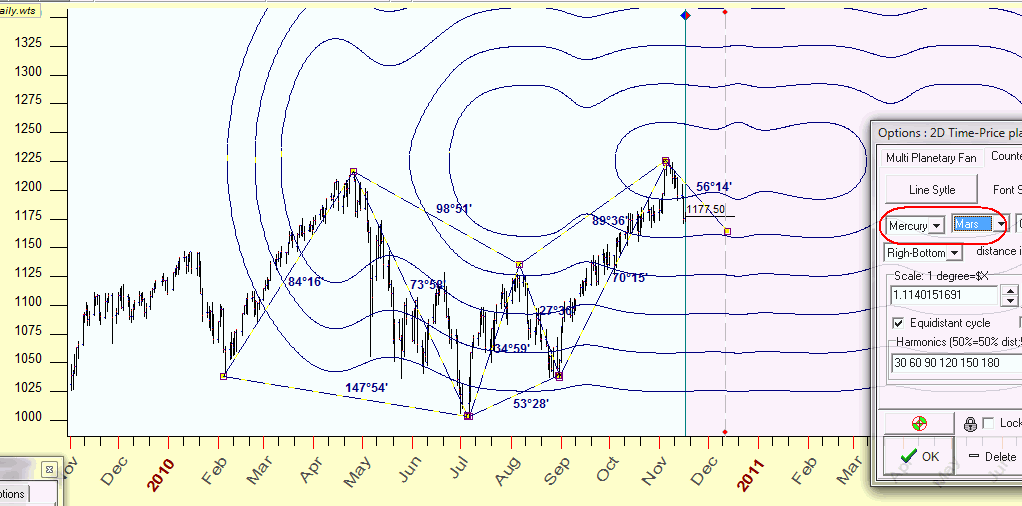
These irregularities caused by retrograde options. Sure this subject needs more researches, much more researches. These last two example I demonstrated as a possible way of future researches.
To draw equidistance cycles focused on the last turning point B, simply draw "2D time-price planetary distance" charting tool starting from the point B to any other point (it does not matter which one) and define harmonic radii there this way:
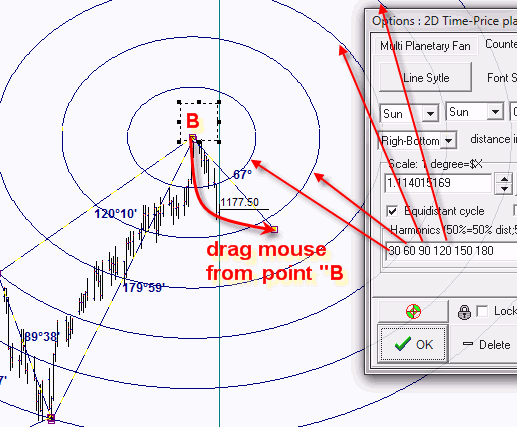
We apply here the newly created charting tool to draw equidistant cycles only.
The worksheet with example that are used in this article is here.
Sergey Tarassov
November 20, 2010
Toronto, Canada