H-Spectrum - cyclical portrait of American stocks for the last 24 years

written by Sergey Tarasov

H-Spectrum: how to do that

H-Spectrum stands for "histogram based" spectrum. To get it, we start with calculating a periodogram. Below is a sample of the periodogram. It represents the cyclical activity, or, we can say, shows the most common cycles that can be found in American stocks price charts since 2000 (i.e. for the last 24 years):

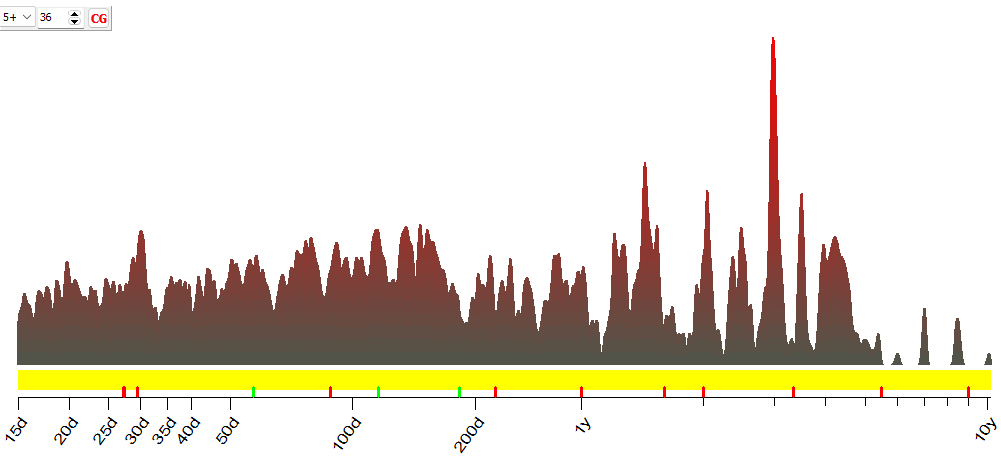
This is a very detailed chart; it involves huge calculations. To get this sample, we have calculated periodograms for 12 American stocks (Bartels-Tarasov algorithm was applied), on different randomly chosen time intervals. By moving the LBC (learning border cursor ), the data interval used for calculations covers a period since the year 2000 till 2024. 

Let us start calculating a periodogram just for one stock. The program automatically has extracted the most important cycles for its price chart; these are seen as peaks on the periodogram. This is how a typical periodogram for one stock looks (JPM; LBC set to April 2020):

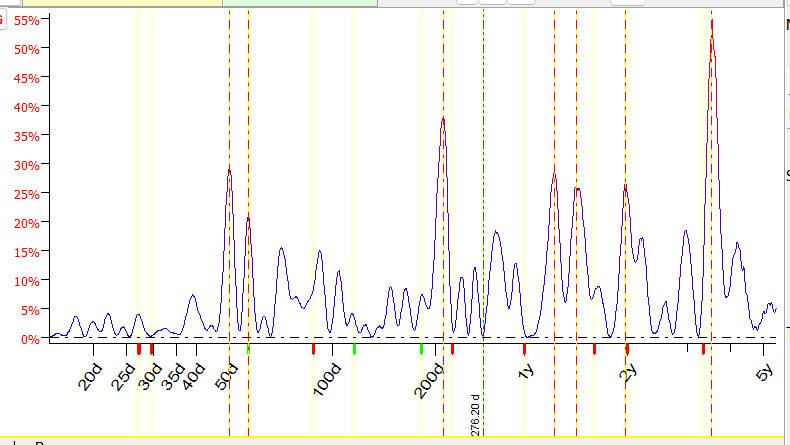
Vertical stripes represent the most significant cycles revealed by the periodogram; its peaks indicate the cycles that accumulate more energy.

We can do the same for any American stock. We can do that for all American stocks, one by one. As a result, we get a huge list of cycles that were found for these stocks. We can get a library of those cycles. We will see there that some cycles appear more often than others. It could be a research project - looking at each cycle separately and selecting those that are relevant for several stocks, groups of stocks, etc. Finding a cycle/cycles that work for many stocks sounds like a promising idea. However, it is too time consuming while its outcome is unclear.

To get some confidence of our results we can display several periodograms together to see what cycles appear more often. Here are four periodograms displayed together; these are calculated for different stocks and LBC positions:

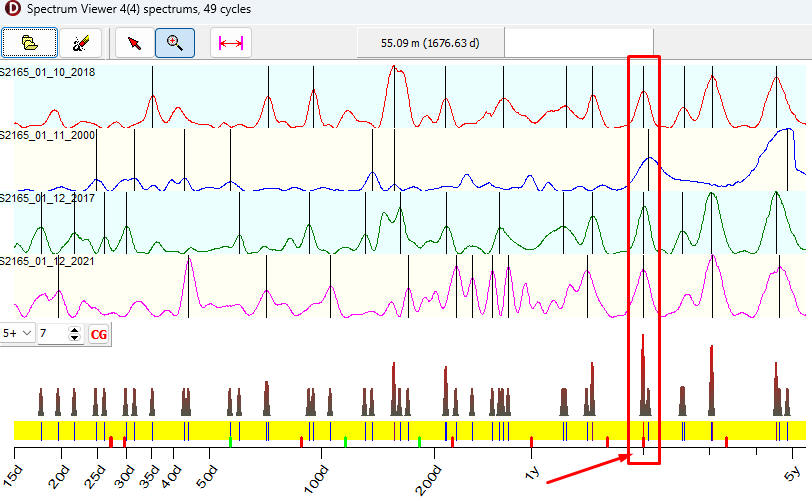
The red chart in the bottom panel is a summary chart. It is called H-Spectrum. As you can see, it shows a peak around 2 years cycle; this peak reflects the fact that this cycle is present in all these four periodograms.

Adding 4 more periodograms, we get H-Spectrum based on 8  periodograms. It reveals 95 different cycles. And you can see there two peaks now, two the most common cycles for these 8 periodograms - 2 and 3-years cycles:

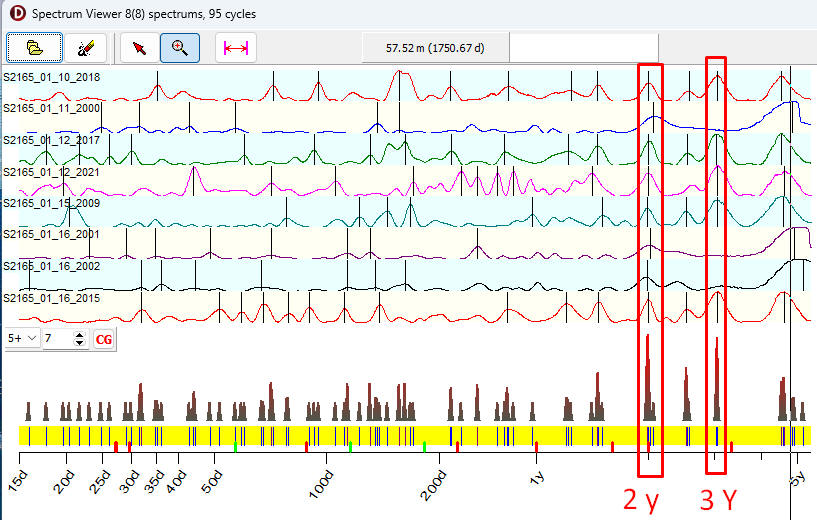
16 periodograms reveal 194 cycles; the final red chart looks even better:

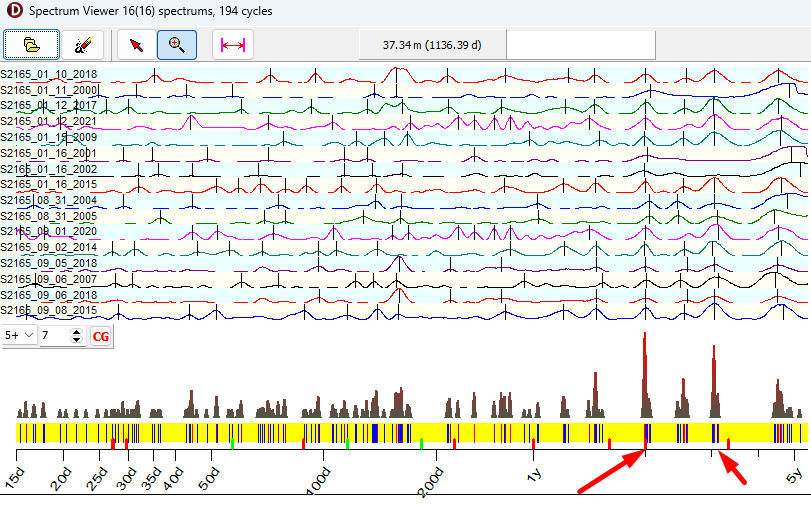
To get the full picture, we have analyzed 4695 periodograms (for different US stocks and different LBC positions). These periodograms take into account 56K cycles. The final histogram is based on 56K cycles; it looks very sufficient from the statistical point of view:

It certainly shows some clusters, some zones where cycles appear more often. 

 I was surprised to find a 3-years cycle as the most often appeared cycle, I expected to see there 40-42 months Kitchin inventory cycle that is revealed by classical cyclical analysis. The Kitchin cycle is present there, it is also strong, though not so strong as 3-years cycle:

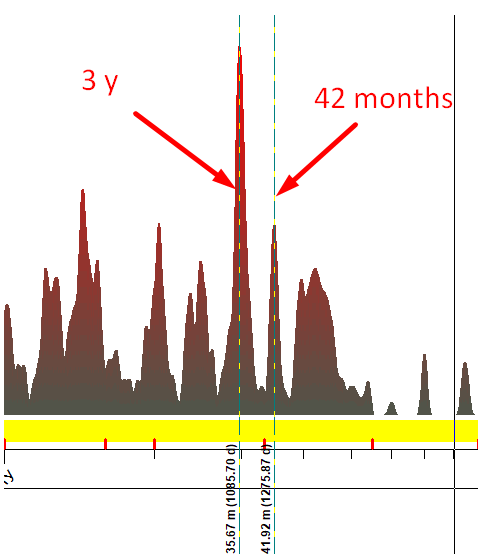
In the demonstrated approach we applied a combination of classical cyclical analysis (by calculating periodograms) and statistical analysis. As the result of this combination, we have got a special type of Spectrum, H-Spectrum. It is a histogram that visualizes a frequency of the appearance of different cycles. This is not a result of some activity of AI (Artificial Intelligence, the software users often ask about that), this is a kind of big data analysis or data mining. 

As to my knowledge, we (Timing Solution team) are the first who applied this approach. In 2017, while working on stocks genome (see this article: https://www.timingsolution.com/TS/Articles/Genome/index.htm ), I tried to present the frequency of cyclical appearance as a histogram chart. It is possible that someone else did that, too, though I have not seen any referral to such approach among scientific papers that were available to me at that time. The closest approach I was able to find is M.S. Bartlett and P.D. Welch's method of averaged periodograms. There is a significant difference there: we analyze histograms for extracted cycles while Bartlett/Welch are focused on smoothing a set of periodograms.

H-Spectrum: H means  Histogram

Soon after the introducing this feature to Timing Solution community, H-Spectrum became one of the most used tools of the Timing Solution software. I would like to explain in details how it works.

H-Spectrum = Histogram Spectrum is, as it is assumed by its name, just a histogram, or the distribution of cycles in regards to their periods.

You can easily visualize the idea of a histogram. Imagine a set of bins. And a big bin with the balls of all sorts and colors, like this one:

The balls in the big bin are a mess. We can sort them, using those empty smaller bins. We put orange basketballs into one bin, baseballs into another, foot balls into the third, red, green, other ones - into other empty bin accordingly. Now we see and we can say how many balls of each kind we have.

The same idea is for the cycles that were extracted from the price charts. We put them into appropriate "bins". Let say that the Spectrum module has revealed a cycle with a period less than 10 days; we put this "ball" into the first bin (have you noticed - I am not using "" for the bin, as it is a regular term for an element of a histogram?). If the cycle's period is between 11-20 days, we put the ball into the second bin. And so on.

Filling the bins, we process all our periodograms/revealed cycles. The most loaded bins correspond to the most common cycles, cycles that appear more often than others.

Usually a histogram is presented this way (this image from Investopedia is included for illustration purposes only; the original was applied for some other need):

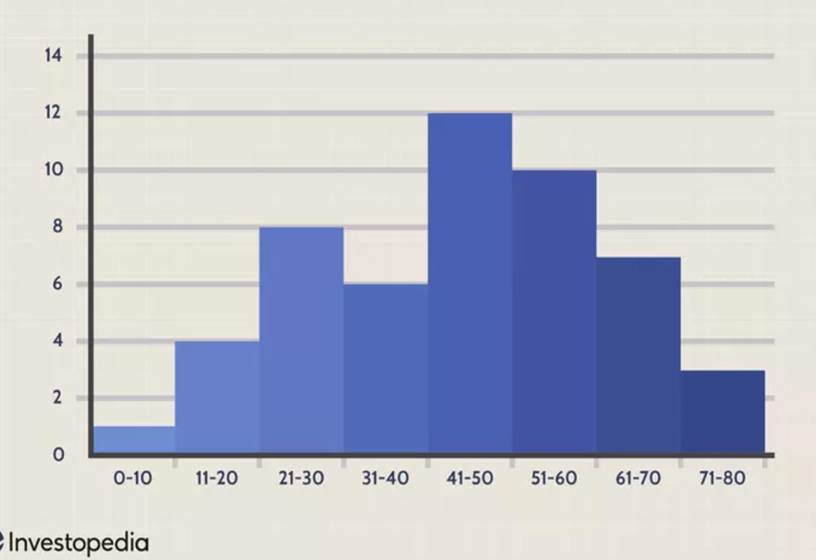
Here the height of the first bin (0-1) is 1; it means that only one cycle with a period no more than 10 days has been found.

Cycles with periods 11-20 days appear more often: 4 of these cycles have been found.

The most typical cycles are 41-50 days ; 12 cycles found, 12 balls in the bin.

Thus you can easily see more or less typical cycles. The amplitude of H-Spectrum just shows how often some cycle appears, it tells you nothing about the amplitude of these cycles.

 H-Spectrum module in action

There are several ways to use H-Spectrum module:

1) H-Spectrum for single instrument (vary LBC only)

Firstly we can apply H-Spectrum for a single financial instrument. Here is an example. I have downloaded Dow Jones Industrial since 1885, opened TS Spectrum module and did this:

It takes 30 minutes to complete these calculations. As a final result we get H-Spectrum for DJIA index. It shows the most typical cycles that appeared in DJIA chart since 1948, i.e. we vary LBC position since 1948 till now (may 2024) and watch the cycles that appear within this period:

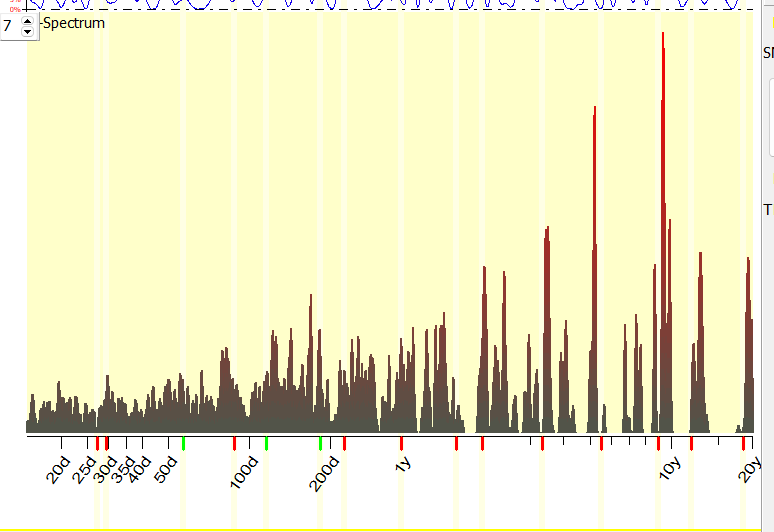
We analyze here temporary cycles, i.e. cycles that live (i.e. can be observed within) some restricted time only. This is why we need to move LBC position to see how historically often these cycles appear.

The chart also shows that we are "in the right direction": practically all the most important cycles revealed by spectrum (they are marked by red arrows) have peaks on H-Spectrum chart:

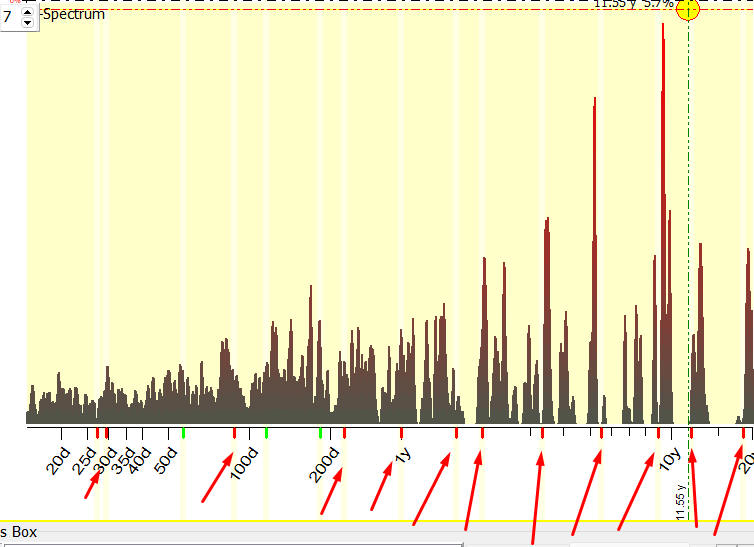
This tool is very good to confirm  economical cycles. It is especially helpful for financial data where the effect of heavy tailed statistic is very important.

Briefly, this effect appears in the situations when we see a peak on some periodogram calculated by classical spectrum. That may be a result of some unusual price movement caused by some extreme and rare event, or it could be a strong cycle that worked for a very short period of time. The statistical significance of this cycle is very low, i.e. with high probability we may consider it as some occasional movement. Still, this peak on periodogram is very high, and we should not ignore it. H-Spectrum algorithm is free of this problem.

2) Multiple financial instruments (vary  financial instruments and LBC)

The application of histograms for cyclical analysis opens some new possibilities. We can calculate H-Spectrum that gathers information from very different sources such as typical periodograms for different American stocks calculated for different time periods. Or another variation: we can calculate H-Spectrum that shows the recent cyclical activity of American stocks based on 1000 American stock charts (this is Cyclical Genome spectrum, available in Timing Solution; it will be explained later). Classical  Bartlett's method of averaged periodograms does not allow to do that.

I would like to remind you about this guy, Maurice Stevenson Bartlett:

Maurice Stevenson Bartlett (1910 - 2002), English statistician

He studied and worked with many great minds of the XX century. He made significant contributions to the analysis of data with specific patterns contained. I have already mentioned Bartlett/Welch method of averaged periodograms. It is the closest that I have found to what we do here. However, this method does not allow to do things that we can do with H-Spectrum. When calculating the averaged  periodogram, we drastically lose spectral resolution, especially on big sample sizes. H-Spectrum works with extracted cycles, not with the periodogram itself. This fact dramatically increases the resolution, especially on big sample sizes. We can take H-Spectrum as an application of Maurice Stevenson Bartlett ideas prolonged into the computer epoch when new computation capabilities became available for researchers.

To calculate our first chart of this article, the chart of cyclical activity for 12 American stocks since 2000 till now. - we have calculated  periodograms for these stocks varying LBC position since 2000 up to May 2024. In other words, we vary here both - the analyzed American stocks and LBC positions. The resulting chart represents the general cyclical picture for American stocks for the last 24 years.

As you can see, the most important cycles here are 30.15 days, 44.18 days, 50.50 days, 57.97 days. and so on; they are marked by vertical lines:

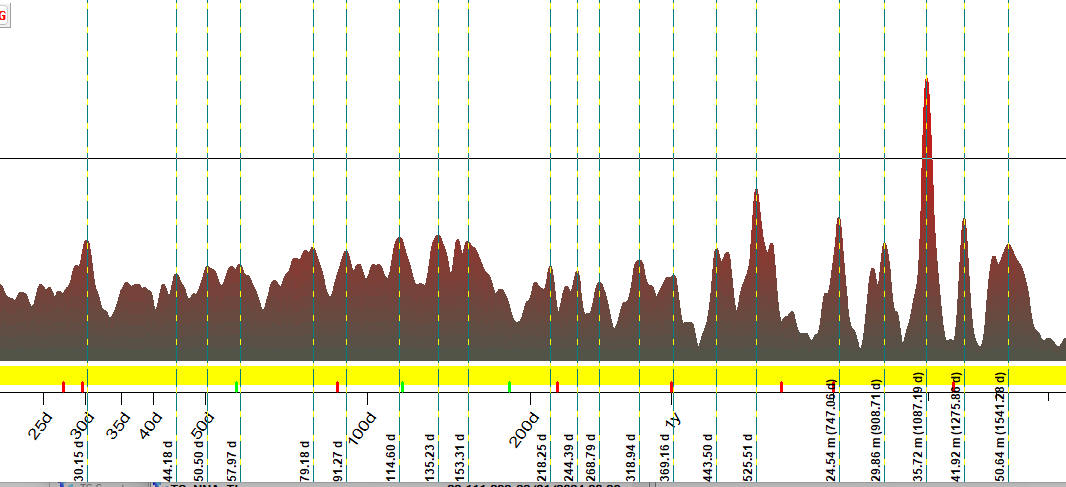
This H-Spectrum is available for Timing Solution software users. It can be downloaded through TS Spectrum module "Cyclical Genome" panel, by clicking this button and choosing the file "Ameerican_Stocks_2000_2024.spectr":

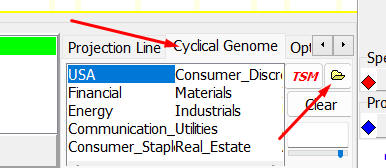
BTW, I have not found any certain confirmation that E.R. Dewey's cycles work. Dewey cycles are marked here by vertical stripes:

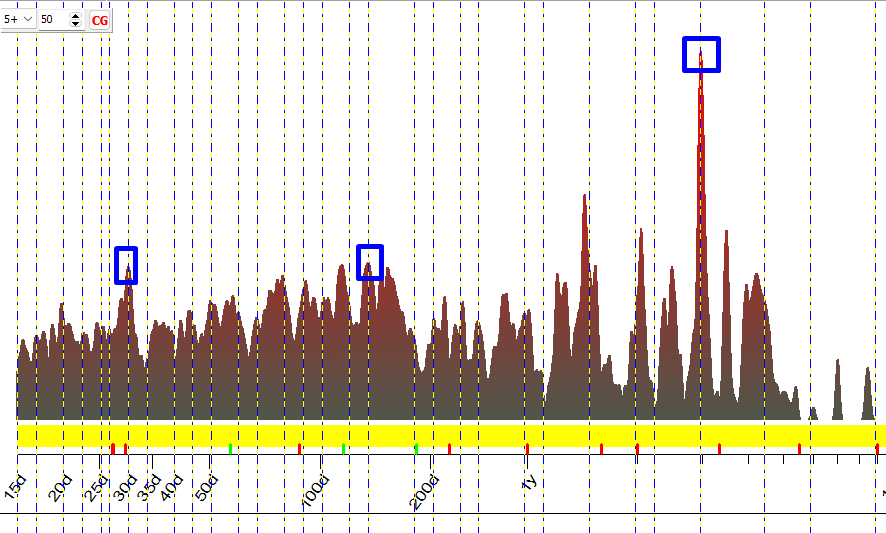
It is possible that I have incomplete information regarding Dewey's cycles. This issue requires more research.

3) Cyclical Genome (vary instruments only)

For traders' needs, this is the most important feature. We do not play here with LBC. We use the latest price history and conduct cyclical analysis for one and the same time period. And we do that for as many stocks (or other financial instruments of the same kind) as we want. In practice, this is what the program does when we work with  Cyclical Genome (CG): it conducts cyclical analysis for some stock on a certain interval (the latest price history is used). As a result, some cycle's presence is detected. Or several cycles. Should we trust this cycle/cycles? Some additional confirmation would be very helpful. In order to get this confirmation, we keep calculating spectrums for hundreds and hundreds of different stocks and watch if this cycle shows up in these stocks.

Look at the chart below. This is Cyclical Genome (H-Spectrum) calculated for 1000 different American stocks. It is created to reveal cycles that worked since March 2023(LBC set to March 2023):

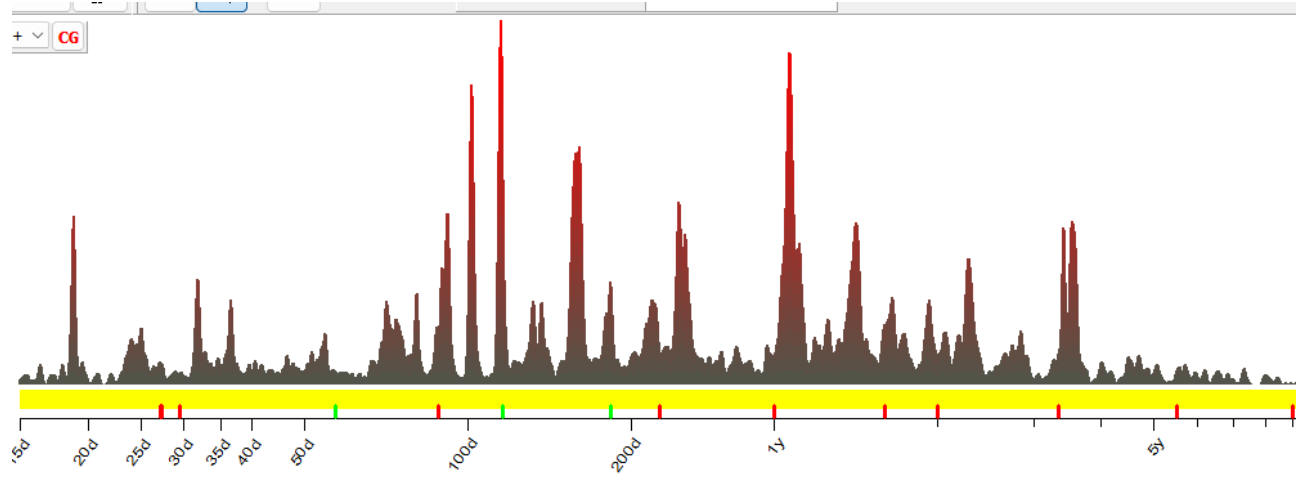
We see here that some cycles are present in the charts of many American stocks. It is not a surprise as the companies operated in the USA are connected in many ways. If there is some cyclical pattern for one company (found by calculating the spectrum for its price chart), it may have some impact on other companies, the vendors or clients of the first one. This is the additional confirmation regarding cycles that we need.

To calculate Cyclical Genomes is an enormous computation task. That is why we perform these calculations aside the software, on a specialized Timing Solution Server machine. 

With the time, the cyclical portrait of stocks is changing. Hence we need to recalculate Cyclical Genome on a regular basis; we do that every other month. This module can be qualified as a big data analysis system.

Instruction for Timing Solution users

Working with H-Spectrum, please remember the following.

Firstly, while you work with TS Spectrum module, you can save a periodogram and extracted cycles by clicking on this button (it saves this info into the file with the extension *,spectr):

This is the way to make your own collection of periodograms, calculating them for different instruments (stocks, etc.) and different time intervals.

To work with these files, use a special utility, Spectrum Viewer.  You can run it through Miscellaneous section:

Here is an example of applying this approach for three major economical indicators.

I have calculated periodograms (using the algorithm that reveals permanent cycles) for GDP, CPI and Unemployment rate and downloaded these periodograms into Spectrum Viewer:

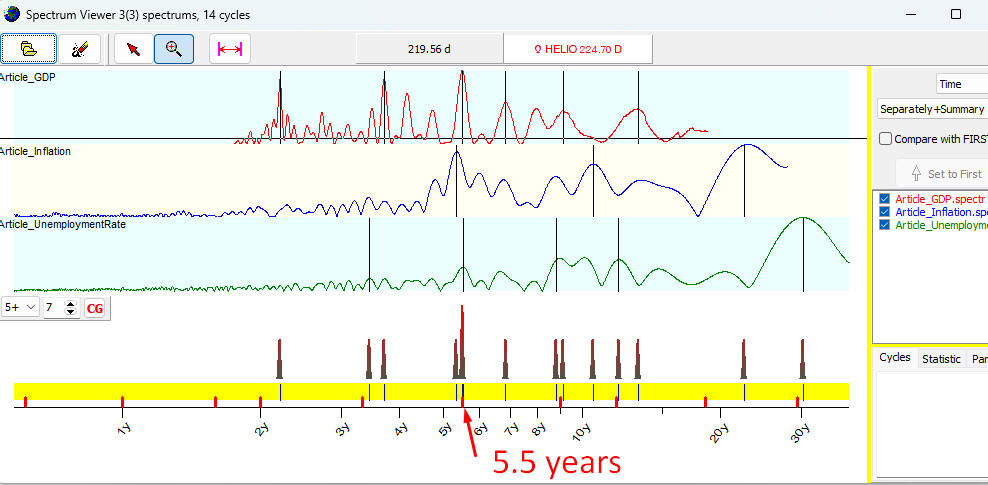
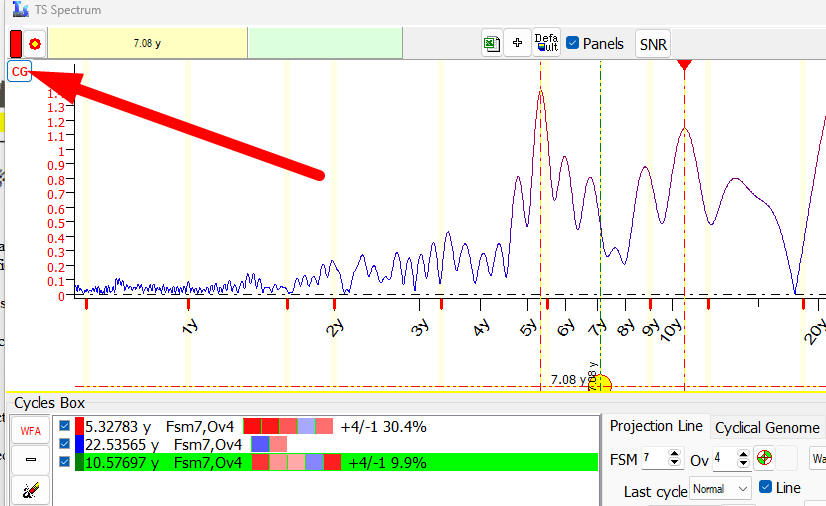
As you see, the cycle with period around 5.5 years works for all these indicators. H-Spectrum displays the highest peak there.

You can download into Spectrum Viewer utility as many periodograms as you need.

For another example, I have downloaded 4695 periodograms. The resulting histogram shows a distribution of 56332 revealed cycles:

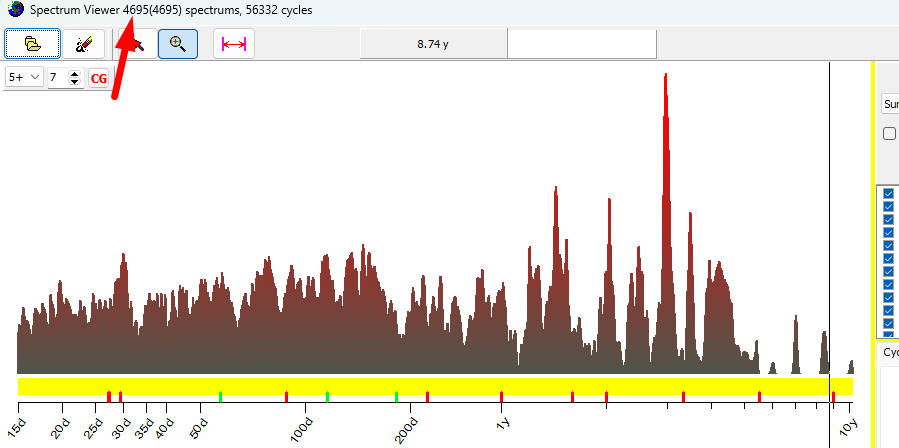
You can save this H-Spectrum into the file clicking this button:

After that, any time you want you can display this H-Spectrum in TS-Spectrum module this way:

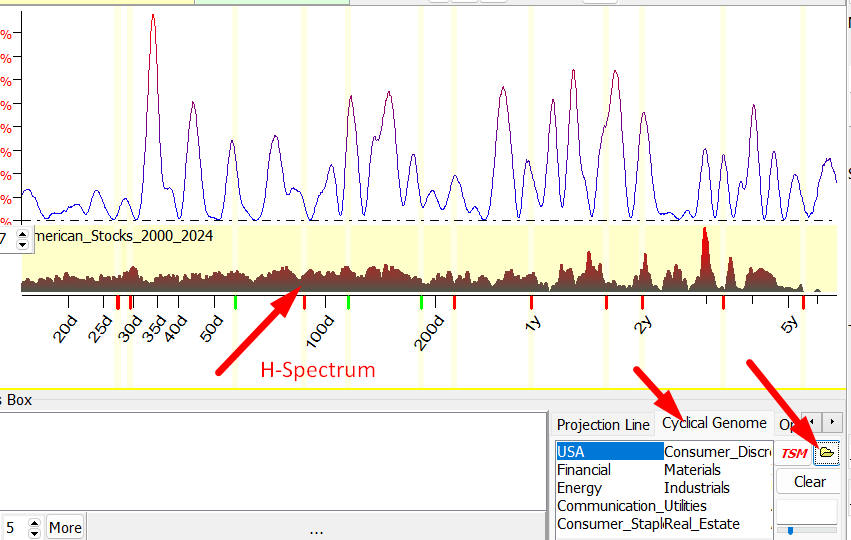
So you can see together the periodogram calculated for your selected financial instrument and H-Spectrum that shows the cyclical activity for the whole market.

May 28, 2024

Toronto, Canada